在计算机科学中,浮点规范化数是数据处理的重要概念之一,随着计算机技术的飞速发展,浮点数的处理变得越来越重要,特别是在处理大量数据、进行高精度计算等领域,本文将介绍浮点规范化数的概念、作用及其在计算机中的实现方式。
浮点规范化数的概念
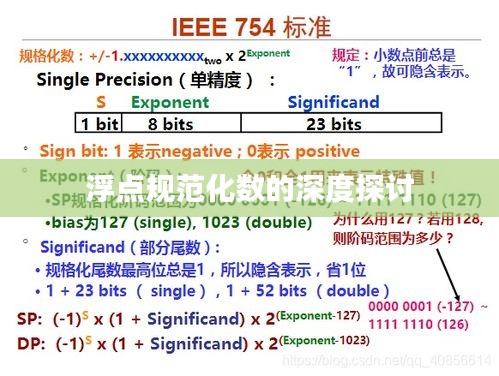
浮点规范化数是一种表示实数的方式,它将实数表示为小数点和指数的组合形式,在计算机内部,浮点数通过特定的格式进行存储和处理,包括符号位、尾数和指数等部分,浮点规范化数的使用可以方便地进行数值计算,尤其是当处理非常大或非常小的数值时。
浮点规范化数的作用
浮点规范化数在计算机科学中发挥着重要作用,它可以表示很大范围内的数值,包括正数和负数,浮点规范化数可以表示很小或很大的数值,而不需要使用大量的存储空间,浮点规范化数还可以进行高精度的数值计算,提高计算的效率和准确性。
浮点规范化数的计算机实现
在计算机中,浮点规范化数通过特定的格式进行存储和处理,一个浮点数包括符号位、尾数和指数等部分,符号位用于表示数值的正负,尾数用于表示数值的精度,而指数则用于表示数值的大小,通过调整这些部分的值,可以表示不同的浮点数并进行数值计算。
浮点规范化数的应用
浮点规范化数在各个领域都有广泛的应用,在科学研究领域,浮点规范化数用于进行高精度计算、数据处理和模拟实验等,在工程技术领域,浮点规范化数用于进行各种数值计算和模拟,如电路分析、信号处理等,浮点规范化数还在计算机图形学、人工智能等领域发挥着重要作用。
浮点规范化数的挑战与解决方案
尽管浮点规范化数具有许多优点,但在实际应用中也会面临一些挑战,浮点数的精度问题可能导致计算结果的误差,为了解决这个问题,研究人员提出了许多解决方案,包括使用更高精度的数据类型、优化算法和采用并行计算等技术,为了处理特殊数值(如无穷大、非数字等),计算机还引入了特殊的浮点数值表示方式。
浮点规范化数是计算机科学中的重要概念,它在数值表示和计算中发挥着重要作用,通过了解浮点规范化数的概念、作用及计算机实现方式,我们可以更好地理解和应用计算机技术,提高数据处理和计算的效率和准确性,随着计算机技术的不断发展,浮点规范化数将在更多领域得到应用,并面临新的挑战和机遇。
转载请注明来自戴码定制,本文标题:《浮点规范化数的深度探讨》











 蜀ICP备2022005971号-1
蜀ICP备2022005971号-1
还没有评论,来说两句吧...